
Since assumption #1 relates to your choice of variables, it cannot be tested for using Stata.
If any of these four assumptions are not met, analysing your data using a Pearson's correlation might not lead to a valid result. There are four "assumptions" that underpin a Pearson's correlation. However, before we introduce you to this procedure, you need to understand the different assumptions that your data must meet in order for a Pearson's correlation to give you a valid result.
#CORRELATION IN STATA HOW TO#
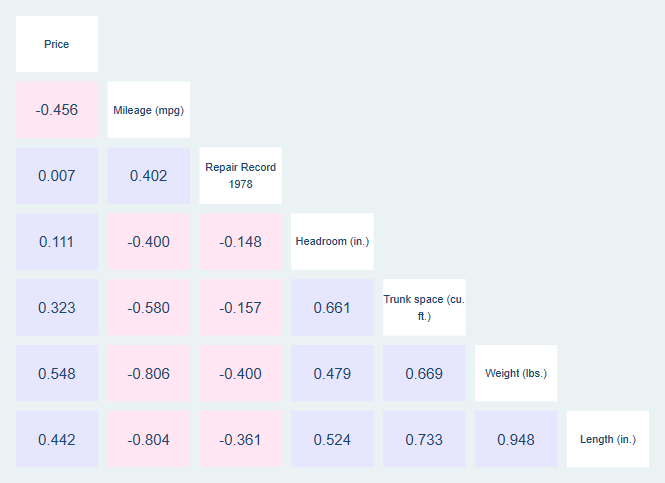
In this guide, we show you how to carry out a Pearson's correlation using Stata, as well as interpret and report the results from this test. If there was a strong, negative association, we could say that the longer the length of unemployment, the greater the unhappiness. Alternately, you could use a Pearson's correlation to understand whether there is an association between length of unemployment and happiness (i.e., your two variables would be "length of unemployment", measured in days, and "happiness", measured using a continuous scale). If there was a moderate, positive association, we could say that more time spent revising was associated with better exam performance. A value of 0 (zero) indicates no relationship between two variables.įor example, you could use a Pearson's correlation to understand whether there is an association between exam performance and time spent revising (i.e., your two variables would be "exam performance", measured from 0-100 marks, and "revision time", measured in hours). Its value can range from -1 for a perfect negative linear relationship to +1 for a perfect positive linear relationship. A Pearson's correlation attempts to draw a line of best fit through the data of two variables, and the Pearson correlation coefficient, r, indicates how far away all these data points are to this line of best fit (i.e., how well the data points fit this new model/line of best fit). The Pearson correlation generates a coefficient called the Pearson correlation coefficient, denoted as r. The Pearson product-moment correlation coefficient, often shortened to Pearson correlation or Pearson's correlation, is a measure of the strength and direction of association that exists between two continuous variables.

We now have a new variable in our dataset called priceres.Pearson's Correlation using Stata Introduction
We’ll call this priceres predict priceres, residuals To obtain the part of price independent of weight and foreign we regress price on weight and foreign. The part of price independent of weight and foreign We can get this information with residuals. We also need the part of mpg that is independent of weight and foreign. To do this we need the part of price that is independent of weight and foreign. Suppose we want to obtain the partial correlation between price and mpg controlling for weight and foreign. Note: Although I’ve only referenced x2, we can in principle include many control variables as our example will show. A semipartial correlation is similar except that we only remove the shared variance between x and x2 (i.e., y remains untouched). Recall that a partial correlation is the relationship between x and y once the shared variance between x and x2 has been removed from x and once the shared variance between y and x2 has been removed from y.
#CORRELATION IN STATA MANUAL#
Partial and Semipartial Correlations – Manual Method


 0 kommentar(er)
0 kommentar(er)
